Introduction
Transformer architecture (Vaswani et al. 2017) has been a milestone for many deep learning application areas, particularly in NLP domain as the backbone of most large language models (LLMs). Scaling up these models has been the key factor allowing them to achieve their high levels of performance and capabilities (Kaplan et al. 2020; Hoffmann et al. 2022). As the models grow larger, trained on more data with increased computational resources, they are able to learn more comprehensive patterns and representations, leading to improvements in understanding and generating human language as well as solving complex tasks (Wei et al. 2022).
The core component of the Transformer architecture is the attention mechanism, which allows embeddings to incorporate contextual information. The standard implementation of the attention mechanism is slow due to its quadratic time and memory complexity and hence becomes a computational bottleneck, especially for long sequences. As a consequence, a primary challenge with scaling up these models is efficiency.
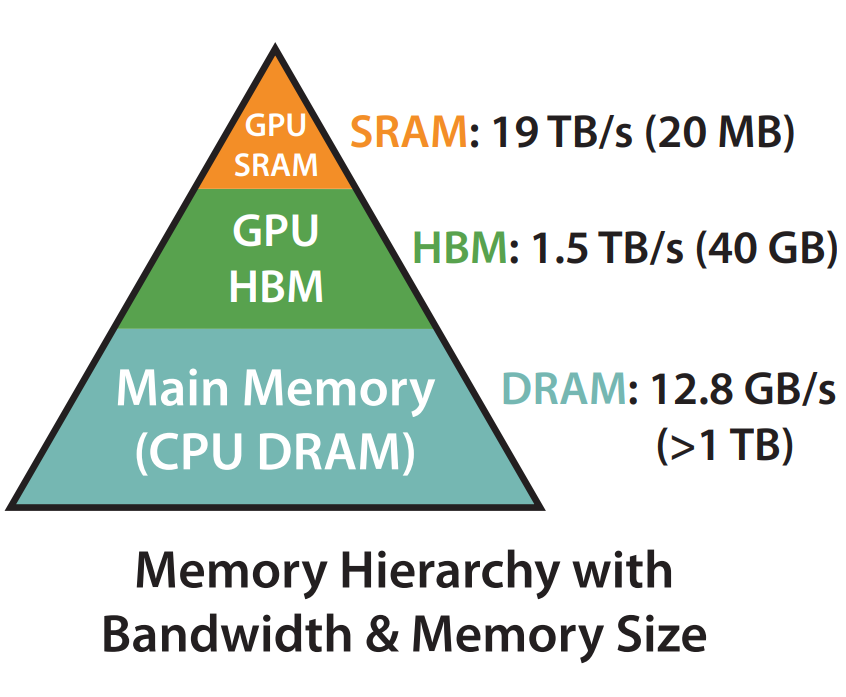
To address this efficiency problem, FlashAttention (Dao et al. 2022) has been proposed as an exact IO-aware attention algorithm. Rather than focusing on reducing the computation of the attention algorithm, FlashAttention reduces the number of IO operations between the GPU’s relatively slow high-bandwidth memory (HBM) and fast on-chip SRAM and effectively utilizes the asymmetric memory hierarchy in graphics processing units (GPUs).
Vanilla Attention
In its simplified form without the scaling factor before applying the softmax, the vanilla attention computation can be written as
\[ O = \text{softmax}(QK^T)V, \]
where $O,Q,K,V ^{N d} $. The vanilla attention algorithm computes the output as following:
Load \(Q\) and \(K\) by blocks from HBM to SRAM | IO operation !
Compute the intermediate result \(S_0 = QK^T\in \mathbb{R}^{N \times N}\)
Write the intermediate result \(S_0\) to HBM | IO operation !
Load *\(S_0\) from HBM to SRAM | IO operation !
Apply softmax to \(S_0\) along the second dimension, which results in the intermediate result \(S_1 = \text{softmax}(S_0) \in \mathbb{R}^{N \times N}\)
Write \(S_1\) to HBM | IO operation !
Load \(S_1\) and \(V\) by blocks from HBM to SRAM
Compute the output \(O = S_1V\)
Write \(O\) to HBM | IO operation !
Even in its most simplified form, attention computation requires data to move between HBM and SRAM several times due to the limited capacity of SRAM, which is e.g. approximately 20 MB in the NVIDIA A100, given it contains 108 streaming multiprocessors each equipped with 192 KB of SRAM (NVIDIA A100 Tensor Core GPU Architecture 2020). Additional memory-bound operations, such as masking and dropout, also increase the IO overhead of the computation.
This demonstrates that the vanilla attention algorithm does not account for the cost of HBM reads and writes, making it IO-unaware. FlashAttention addresses this problem.
Flash Attention
In contrast to the vanilla attention algorithm, FlashAttention computes exact attention with fewer HBM reads and writes. It achieves this by applying two well-established optimization techniques: tiling and recomputation. The key idea behind FlashAttention is to avoid materializing intermediate matrices and to fuse all CUDA kernels (matrix multiplication, softmax etc.) used in the vanilla attention computation into one as depicted in Figure 3.
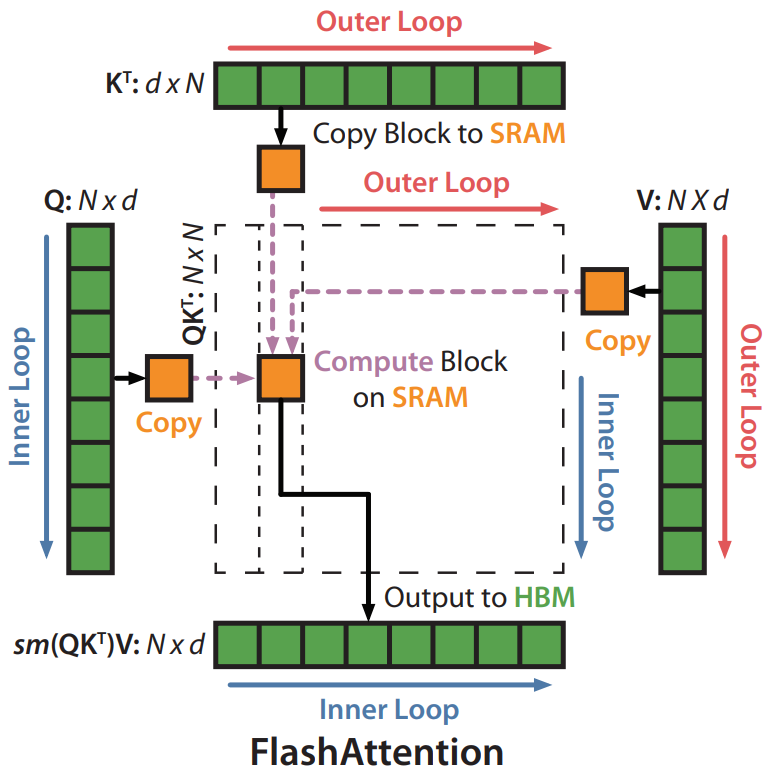
Tiling
A major challenge in tiling the attention computation lies in the non-associative nature of the softmax function. Traditionally, softmax of a vector \(x \in \mathbb{R}^d\), which can be thought as a row of the intermediate result \(S_0\), is computed using an algorithm called “safe softmax” for numerical stability as in Figure 4.

The problem with using safe softmax while computing the attention is that it requires three iterations over the entire input vector \(x\): one iteration to determine the maximum value \(m\), one iteration to calculate the normalizer \(l\) and one iteration to calculate the final output \(o\). This, consequently leads to reads/writes from/to HBM since SRAM does not have enough capacity to materialize the entire intermediate matrix. On the other hand, online softmax (Milakov and Gimelshein 2018) depicted in Figure 5, offers an alternative to safe softmax to calculate the maximum value \(m\) and normalizer \(l\) in an online manner in a single loop.

Although computing the attention matrix \(S_1\) with the online softmax still requires two loops and hence a read/write from/to HBM, it is not necessary to materialize the attention matrix \(S_1\) to compute the output of the atttention \(O = S_1 \cdot V\). Thus, the output can be computed in blocks directly in a single loop with a low memory footprint that fits into the SRAM. The derivation and details of this single-loop computation are beyond the scope of this review and are left to the reader for further reading (Ye 2023).
Recomputation
In the context of performance optimization, recomputation refers to the concept that, in certain scenarios, recomputing data may be faster than storing intermediate results and accessing them from memory. As we discussed in Tiling, FlashAttention avoids materializing the intermediate matrices \(S_0\) and \(S_1\). As a consequence, it can also not read the intermediate matrices during the backward pass, as they are never materialized and stored. Instead, FlashAttention stores the softmax normalization statistics \(m\) and \(\ell\) and recomputes the \(S_0\) and \(S_1\) to compute the gradients of \(O\) with respect to \(Q, K\) and \(V\). Although recomputation results in more FLOPs, it improves the wall clock time of the algorithm, as the slow HBM is accessed fewer times.
Experimental Results
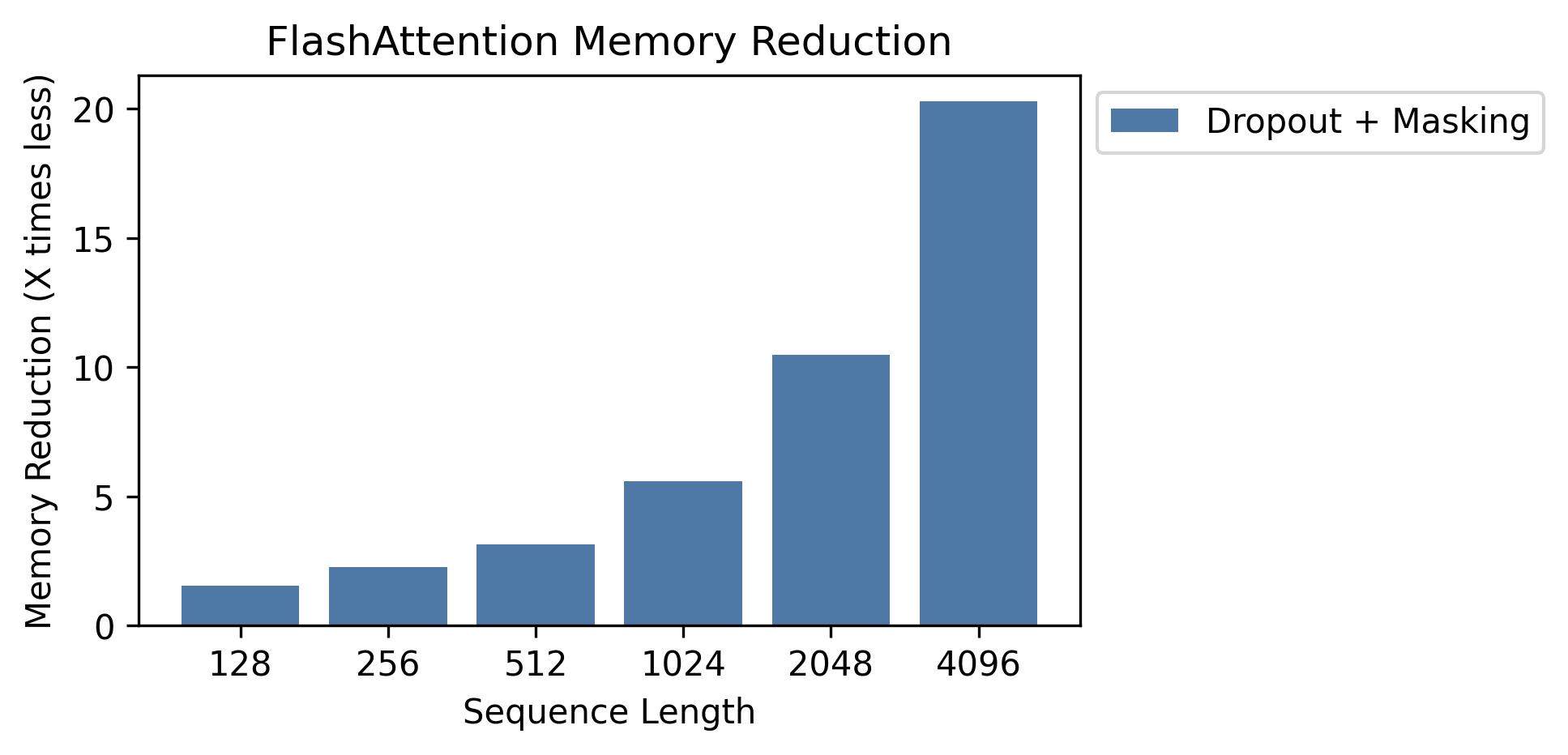
In this section, we analyze the experimental results of the FlashAttention.@fig-flashattn_memory demonstrates the reduction in HBM memory usage compared to the vanilla attention algorithm. Since FlashAttention does not materialize the \(N \times N\) intermediate matrices, it only requires \(O(N)\) additional HBM memory for the output and softmax statistics as opposed to \(O(N^2)\) memory requirement of the vanilla attention algorithm. This results in a quadratic increase in memory reduction with respect to the sequence length \(N\).
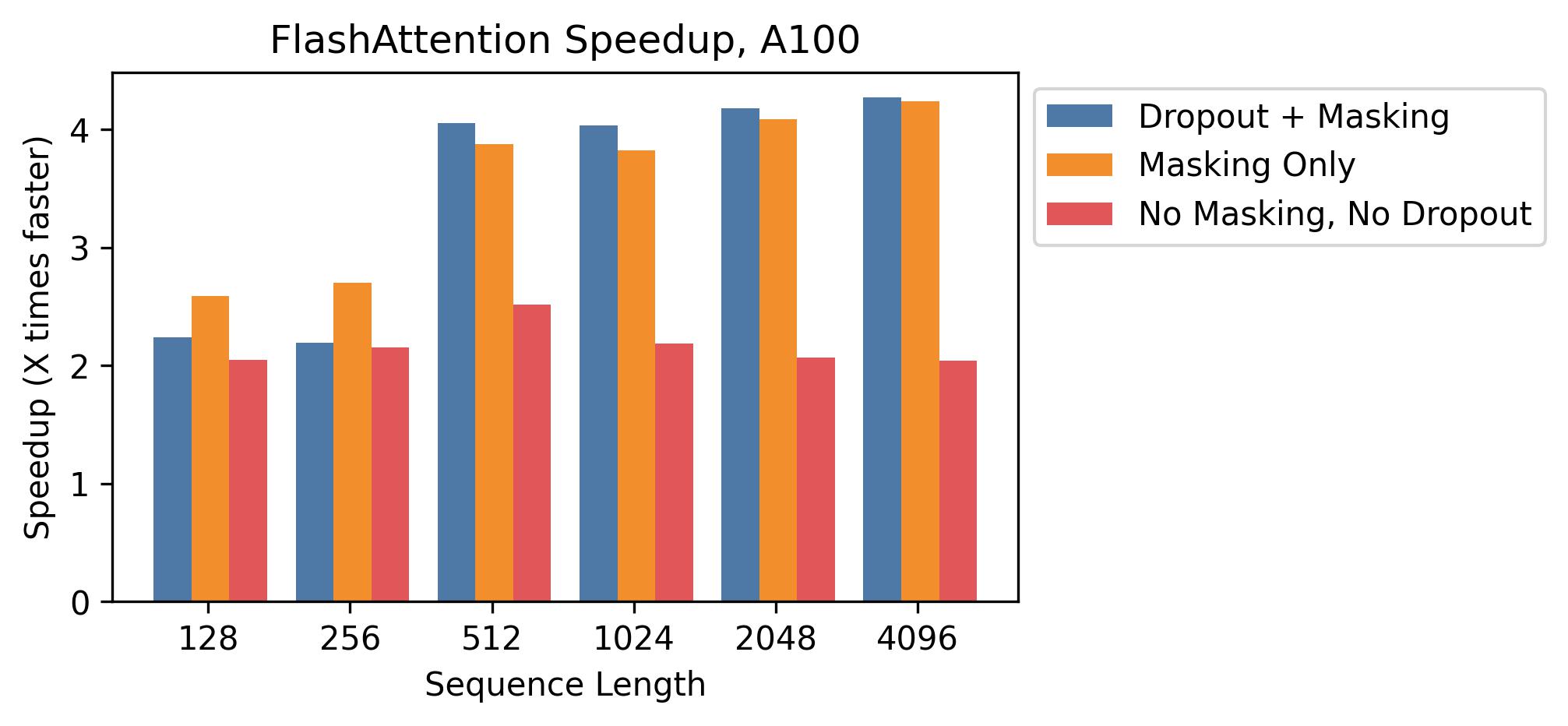
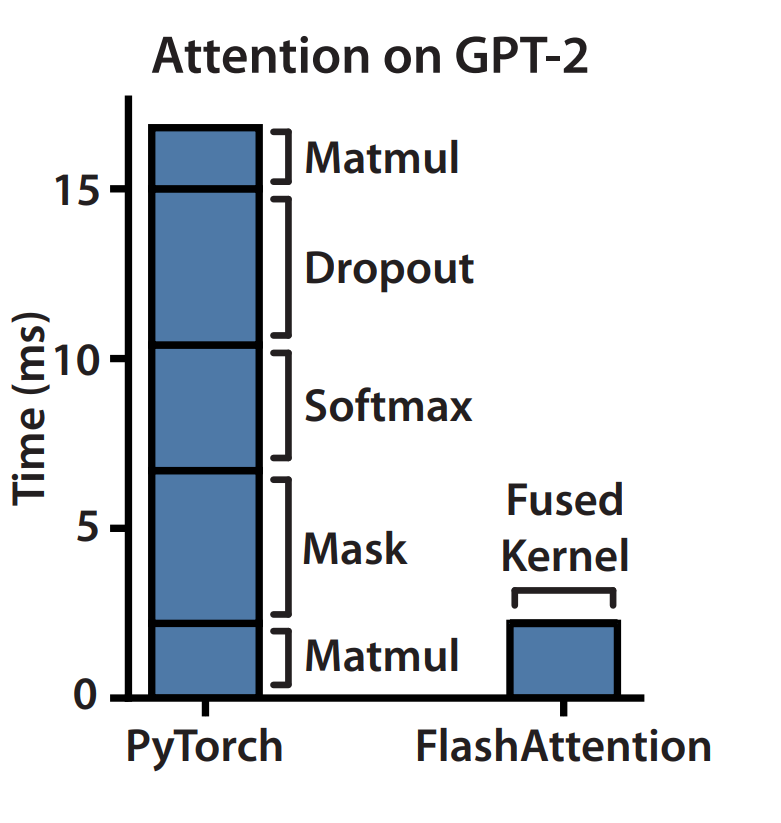
In addition to memory reduction, FlashAttention is also faster compared to the vanilla attention algorithm as depicted in Figure 7. The speedup is particularly significant when optional dropout and masking operations are applied during the attention computation. This behavior is expected, as the optimizations employed in FlashAttention aim to reduce the I/O complexity of the vanilla attention algorithm. Memory-bound operations, such as masking and dropout, are the primary sources of bottlenecks in terms of wall clock time.
Personal Comment
“Attention is All You Need” (Vaswani et al. 2017) in 2017 marked a pivotal moment, establishing the Transformer architecture and attention mechanism as fundamental building blocks for many groundbreaking research endeavors and widely-used products. What, I find particularly interesting about FlashAttention is how, despite several years of research in one of the most rapidly evolving scientific domains, such an elegant yet “simple” line of optimization could be overlooked for arguably one of the most crucial operations. This is especially surprising given the significant financial incentives and vast resources available to companies that would benefit from an algorithm such as FlashAttention. Of course, hindsight is 20/20.
By the way, FlashAttention 2 (Dao 2024) and FlashAttention 3 (Shah et al. 2024) are available as even more optimized attention kernels, and their adoption has been widespread across the industry. In that regard, I have become a big fan of Tri Dao’s research. I understand that academic and industrial research are driven by different motivations, but I believe more academics should pay attention to real-world use cases and their computational constraints.